
Getting financing into perspective
Not counting the speculative investors and the various kinds of capital that might be introduced at the birthing stage of an e-business startup, all other forms of financing need to have some basis in rationality.
This basis must, in some way, be related to the four cornerstone concepts of finance and investment calculation:
1) Discounting through time
2) Turning an income into a capital value
3) Turning a capital amount into an income stream
4) Discounting for risk
It is worth noting that all banking, insurance, pension and investment industries are based solely upon these four important concepts. All financiers, and anyone seeking finance, should fully understand the conceptual mind set they represent.
Discounting through time
Discounting through time is the calculation necessary to be able to turn income into capital and capital into income. It's basic premise is that a sum of money in the future is worth less than that same sum of money in the present.
The best way to imagine this is to think of a visual image. Up close it appears large. As the image moves further and further away it gets smaller and smaller. Substitute money for the image and distance for time and you have a good visualisation as to how the value of a sum of money shrinks the further away it is from the present day.
It may seem impossible that a sum of money can reduce in value as it appears further away in time. After all, if you put ten thousand dollars under the mattress and fetched it out after ten years, it would still be the same ten thousand dollars.
However, the factors influencing present and future values are:
1) Inflation, which can cause the actual value to shrink
2) The risk of some unexpected disaster occurring whereby the money gets lost.
3) The money in the present can be profitably invested so that it will increase in value by a future date due to compound interest.
This can be imagined by thinking of two people, each with ten thousand dollars. One puts it under the bed for ten years, the other invests the money in safe securities that pays an interest of 7.2 % per annum which adds each year to the total amount (compound interest). What happens to the values of their respective savings is detailed in figure 1.
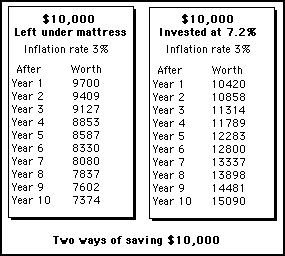
Figure 1 - Showing how the value of money changes over ten years according to how it is saved
As can be seen from figure 3.1, money not put to work can decrease in value due to inflation. Money invested can increase in value due to compound interest. With inflation at 3% (affecting both ways of saving) and the investment paying 7.2% per annum interest, after ten years the invested money is worth about double the money put under the mattress.
All financial business decision making is based upon being aware of these differences between a present day value and a future value of money. The concern is not only with how much a sum of money will grow to at some time in the future, but, also how much a future sum is worth in the present. For example, the table in figure 3.1 tells us that a sum of $15,000 dollars in the future is worth $10,000 today because $10,000 will turn into $15,000 over ten years.
Being aware of the way in which a future value seems to shrink as it is brought back to the present allows an important financial calculation to be made. It allows incomes to be given capitalised values. This is illustrated in figure 2, where an income of $100 dollars per annum stretching over the next 100 years can be given a value by adding up all the payments discounted through time back to the present day.
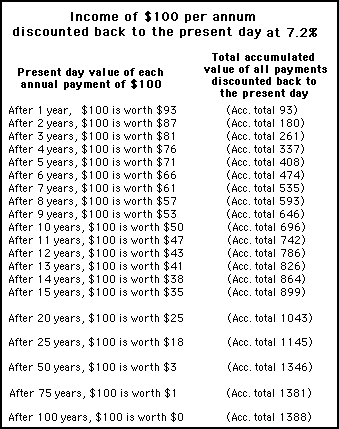
Figure 2 - The value of an income can be calculated by discounting the value of each payment back to the present day and totalling up these discounted values
From figure 2, it can be seen that an income over one hundred years has a finite value because the present day value of future payments gradually reduce to zero. In this example, where the interest is assumed to be 7.2%, it can be seen that the capitalised value of an income of $100 per annum approximates to just under $1,400.
Similarly, an income of $10,000 per annum would be valued at $140,000. An income of $100,000 per annum would be valued at $1.4 million. It is through this kind of calculation that the value of a company's equity shares can be valued. If you can estimate the rate of earnings, you can get an idea of the basic value of its shares and therefore its share price.
Of course it is not quite as simple as this because there is an element of guesswork in assuming the correct percentage to use for the discounting. There is also a guess that has to be made as to what the rate of inflation will be. This allows wide differences in opinion as to the correct value of any particular income: according to what values are assumed for the discount and inflation rates. Figure 3 shows how an income of $100 per annum might be valued assuming different discount rates.

Figure 3 - The value of an income will be valued differently according to what discount rate is used. A discount rate of 5% will value a $100 per annum income at $1,985, but, at a discount rate of 50% the value be only $199