
Scaling up
The hypothetical example described above assumes a limited number of merchants and garment buyers. The number of merchants in each garment space is assumed to be quite modest, such that it would be possible for buyers in the space to easily contact all of them to sort out who is the best to deal with.
However, if this were extended world wide, to include every merchant on the planet and everyone in the world is allowed to join in, the system would soon become overcrowded. There might be thousands of merchants in the garment spaces and it would be very difficult for buyers to choose between them.
To make life easier, it might be sensible if each garment space were divided up further. Perhaps divided by geographic location. This would reduce the numbers in any particular space and at the same time ensure that buyers didn't waste time trying to deal with merchants whose warehouses were further away than they were prepared to travel.
By splitting up the garment spaces in this way the total space would take the form of a two dimensional grid, as shown in figure 8. In this diagram, there are twelve garment spaces (columns) divided up into twelve geographic locations (rows). This creates 144 different spaces where merchants and buyers can meet.
In each of these areas, there will be fewer people, but, they will each know that they are interested in the same kind of garment and are geographically close to each other.

Figure 8 - Contact places, where merchants and buyers meet, can be spread over a two dimensional grid to increase the efficiency of finding the best contacts
Even though there might be a large number of garment categories and a large number of geographic locations, some of the contact areas might still be over crowded. This problem is easily overcome by adding yet another dimension to the overall meeting spaces.
Let's say that the type of locality, where the merchant's warehouse is situated, is also an important buying consideration. This is illustrated in figure 9 where by adding twelve categories of locality, the total number of possible contact points is increased from the two dimensional number of 144 to a three dimensional number 1,728.
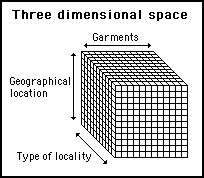
Figure 9 - By adding a third dimension, the possible contact places have increased from 144 to 1,728
Adding this third dimension, not only reduces the over crowding, but, also ensures that buyers and sellers are more likely to be compatible.
Imagine now that there are thousands of different merchants of many different nationalities and customers only speak one language. They would obviously prefer to deal with only the merchants that they can speak with. This can be accommodated by adding a fourth dimension, which will create a different three dimensional space for every language. This four dimensional space is illustrated in figure 10, where the three dimensional space is recreated ten times: each to cater for a different language that the merchants and customers might prefer to speak.
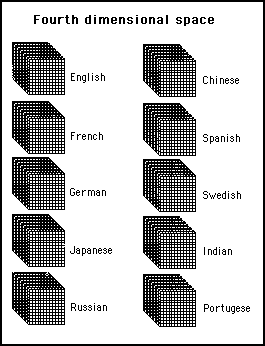
Figure 10 - By adding a fourth dimension, customer can go to the spaces where they'll meet only the merchants who speak their language
This fourth dimension will have the effect of increasing the number of different possible meeting places to 17,280. This will greatly reduce the effect of over crowding and at the same time improve the compatibility of buyers and sellers.
There may be other preferences that a customer might have. If there are so many merchants that that there is still over crowding, a new dimension can be added for every important category. Figure 11 shows a fifth dimension being added to allow the customer to also choose the size of the merchants they deal with:

Figure 11 - A fifth dimension might separate out the merchants by the number of outlets they have, as well as by garments supplied, geographic location, type of locality and language spoken. In this diagram, it shows this fifth dimension as consisting of nine groups, each with ten, three dimensional areas
This fifth dimension will increase the number of different places a merchant or a buyer can establish a presence in to 155,520. This may seem ludicrously excessive for finding garment merchants, but, this is only a simple: example used to explain the principle. What is of interest is that this same principle can be applied to subject areas where there are millions of people involved. Then, 155,520 different possible meeting places might seem very sensible indeed.
These diagrams graphically illustrate how the parameters associated with choice can be used to format a people space to increase the efficiency of finding suitable contacts. The significance of this model cannot be underestimated. This is a powerful way to divide up a super large population in order to seek out valuable contacts for information or help.